2. 南昌大学第一附属医院泌尿外科, 南昌 330006
2. Department of Urology, First Affiliated Hospital, Nanchang University, Nanchang 330006, China
生理状态下,尿液自输尿管流入膀胱,这很大程度上归功于输尿管膀胱壁内段Waldeyer鞘的单向瓣膜作用[1]。膀胱输尿管反流(vesicoureteral reflux, VUR)是指尿液从膀胱逆流至上尿路,是婴幼儿泌尿道感染(urinary tract infection, UTI)的常见病因之一,约20% ~40%的婴幼儿发热性UTI可出现VUR。反复发作尿路感染可形成肾瘢痕,继而导致肾功能损害,如得不到有效控制,最终可导致高血压和终末期肾病[2]。针对高级别VUR、肾瘢痕及预防性使用抗生素无效的患儿,手术是保护患儿肾功能的有效手段。常见手术方式包括膀胱内途径的Cohen术、Politano-Leadbetter术和Glenn-Anderson术以及膀胱外途径的Lich-Gregoir术。手术的关键在于建立一个膀胱黏膜下隧道以延长黏膜下输尿管长度,形成新的抗反流机制[3]。目前在处理黏膜下输尿管长度上,较为公认的是Wein等[4]推荐的方案,即隧道长度取决于输尿管直径,建议长度与输尿管直径的比例为5:1。
有限元分析(finite element analysis, FEA)是以计算机为工具,利用数学近似的方法模拟真实物理系统。它将复杂的物理系统看成是由许多有限元的小的互连子单元组成,对每一单元求得近似解,然后推导模拟出其总的真实状况。由于其计算精度高及近年来计算机技术快速发展,FEA已经从最开始的工程分析手段扩展到几乎所有科学技术领域。
本研究基于ANSYS软件建立不同的膀胱输尿管模型,利用FEA方法分析膀胱输尿管在不同载荷下的等效应力及位移,阐述黏膜下输尿管抗反流机制,为VUR的手术治疗提供理论依据。其中,等效应力是指有限元模型中各个节点的各应力分量经适当组合而形成的与单向应力等效的应力。
资料与方法参考正常膀胱输尿管的生理结构参数,在ANSYS 2020 R2软件中构建膀胱输尿管结构模型。其中,膀胱为容量300 mL的近椭圆体,长轴64 mm,短轴44 mm,膀胱黏膜层1 mm,肌层4 mm;输尿管隧道直径2 mm,模型中设置不同的隧道长度及深度,包括A1型(长宽比3:1)、A2型(长宽比5:1)、A3型(长宽比7:1)、B型(肌层隧道,长宽比5:1)、C型(斜形隧道)、D型(垂直隧道),并进行有限元分析处理。采用补丁适形算法将模型划为四面体网格,考虑到输尿管隧道周围区域的复杂性,这里的网格数量明显高于其他地方,以减少误差;并对各部分材料进行杨氏模量的赋值(膀胱黏膜层150 kPa,输尿管100 kPa,肌层50 kPa)[5]。
基于正常生理状态,将膀胱模型底部进行固定约束,载荷分为储尿期与排尿前期两部分。其中,储尿期膀胱压力为20 cm H2O(1 cm H2O=0.098 kPa,加载于膀胱黏膜层),逼尿肌压力及腹压为0,以模拟膀胱舒张过程;排尿期膀胱压等于逼尿肌压与腹压之和,为80 cm H2O(加载于膀胱肌层),尿道内压力为50 cm H2O(加载于膀胱黏膜层)以模拟膀胱收缩过程,均为线性增加至最大载荷[6]。分析设置中采用自动时间步长,初始子步100,最小子步100,最大子步1 000,并开启大绕曲,在求解方案中开启自适应网格加密,最大加密循环3,加密深度3,最后计算等效应力及位移分布情况。
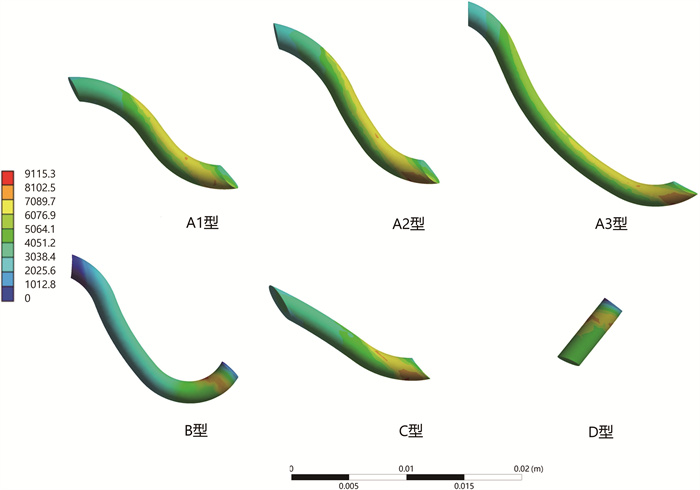
结果 一、储尿期等效应力分布云图及位移分布云图储尿期载荷下,不同隧道模型的输尿管壁内段最大等效应力变化并不明显(表 1)。等效应力分布云图显示,最大等效应力均位于黏膜与肌层交界处(图 2)。A1、A2、A3型黏膜下隧道部分有较高的应力分布。A1型隧道短于A2型,但其隧道段的最大等效应力只比A2型低1%。A3型隧道长于A2型,其隧道段的最大等效应力比A2型高出3%。B型虽然和A2型有着相同的隧道长度,但其隧道上的应力分布及隧道段的应力差均远远低于A2型,较A2型减少了46%(表 2)。D型有着最大的等效应力峰值,但根据位移分布云图显示,其隧道呈现扩张趋势,其余4种隧道均呈现收缩趋势,其中A1、A2、A3型最为明显(图 3)。

|
图 1 输尿管隧道仿真模型 Fig.1 Ureteral tunnel simulation model 注 黄色:膀胱黏膜;灰色:膀胱肌层;绿色:输尿管隧道 |
| 表 1 储尿期及排尿期不同隧道模型的输尿管壁内段最大等效应力(Pa) Table 1 Maximal equivalent stress (Pa) of ureteral-bladder segment under different tunnel models during urine storage and urination periods |
|
|
|
图 2 储尿期不同隧道模型的等效应力分布云图 Fig.2 Equivalent stress distribution cloud diagram of different tunnel models during urine storage period |
| 表 2 储尿期及排尿期不同隧道模型的隧道段最大等效应力(Pa) Table 2 Maximal equivalent stress (Pa) of tunnel segment under different tunnel models during urine storage and urination periods |
|
|
|
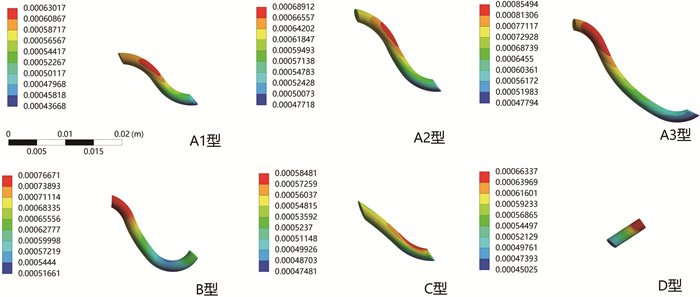
图 3 储尿期不同隧道模型的位移分布云图 Fig.3 Displacement distribution cloud diagram of different tunnel models during urine storage period |
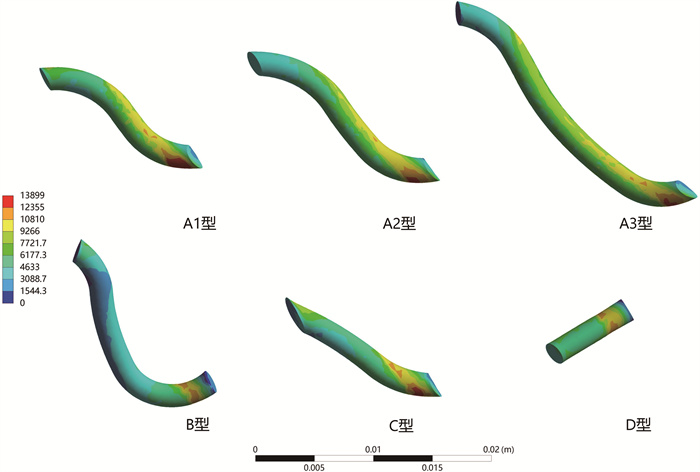
排尿期时,不同隧道模型的最大等效应力均高于储尿期,但各型之间变化仍不明显(表 1),其等效应力分布特点类似于储尿期(图 4)。不同的是,在位移分布上,D型与其他4种隧道一样呈现收缩趋势(图 5)。A1型隧道虽较A2型短,但其隧道段的最大等效应力比A2型高出9%,A3型比A2型高12%,而B型相比于A2型减少53%(表 2)。
|
图 4 排尿期不同隧道模型的等效应力分布云图 Fig.4 Equivalent stress distribution cloud diagram of different tunnel models during urination period |
|
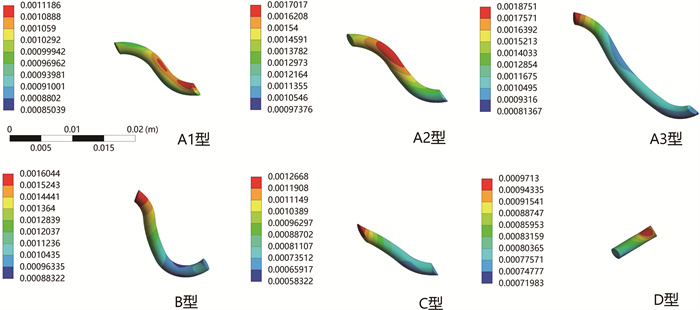
图 5 排尿期不同隧道模型的位移分布云图 Fig.5 Displacement distribution cloud diagram of different tunnel models during urination period |
文献报道约有80%的Ⅰ、Ⅱ度低级别VUR和30% ~50%的高级别VUR伴随生长发育而自行缓解,这是临床上采取持续口服抗生素预防(continuous antibiotic prophylaxis, CAP)治疗的主要依据[7-8]。但如果在CAP治疗中出现突破性UTI或者长时间高级别反流,则患儿仍需接受手术治疗[7]。另外,内镜下注射治疗也被认为是安全有效的抗反流治疗手段之一[9-10]。目前较为主流的手术方式均以建立黏膜下隧道为主要目标,但受限于当前检查技术无法对其进行有效的生物力学分析。有限元分析有着无创、精确、可重复性好等优点,可弥补现有技术的不足。本研究通过有限元分析模拟膀胱收缩与舒张过程中输尿管隧道的等效应力及位移分布情况,为抗反流手术提供可靠佐证。
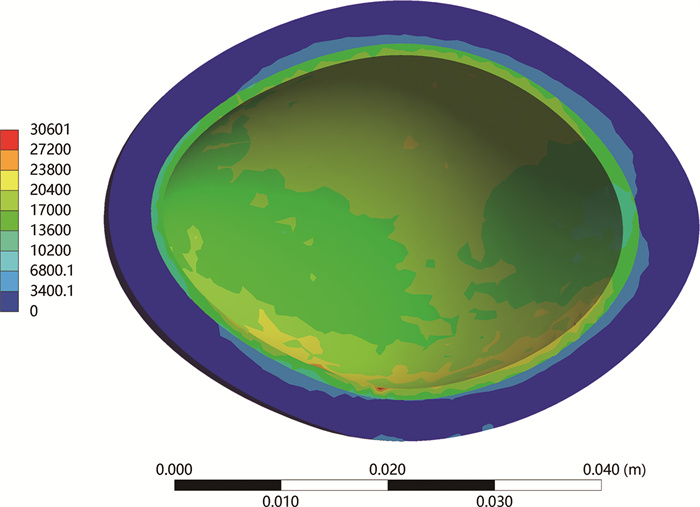
模拟结果显示,所有模型输尿管壁内段的最大等效应力均位于膀胱黏膜与肌层交界处或输尿管转折处,这可能是术后输尿管狭窄的高发部位。无论是储尿期还是排尿期,黏膜下隧道(A1、A2、A3型)均有着较高的应力分布,三者的最大等效应力差别不大,但明显高于肌层隧道(B型),这是因为黏膜与肌层之间有着明显的应力变化,但肌层内部应力变化较为平缓(图 6)。这突出了黏膜下隧道在术后抗反流作用中的关键地位。
|
图 6 排尿期膀胱壁等效应力分布云图 Fig.6 Equivalent stress distribution cloud diagram of bladder wall during urination period |
有限元分析在泌尿外科有着大量应用研究,Kim等[11]等通过有限元分析中的计算流体力学模型分析了双J管置入后输尿管反流的主要影响因素为逼尿肌的开放状态及输尿管的狭窄程度,并为抗反流双J管的设计提供了方案。近年来,不断有研究人员向Wein等[4]推荐的长径比提出挑战。Villanueva等[12]研究认为,输尿管口的构型对反流起着至关重要的作用,隧道的长度对于闭合压力并没有直接的影响。Kalayeh等[13]通过对输尿管再植术中输尿管的有限元分析认为,Paquin观察到的长径比是抗反流手术的主要机制,但由于膀胱膨胀时的拉伸作用,手术时的长径比与Paquin所描述的并不相同,在接近容量(膀胱容量的80%)时手术实施的5:1长径比相当于静止时的7:1,术者在手术时可能过度选择了长径比。本研究也得出了类似的结论,即无论储尿期还是排尿期,随着黏膜下隧道长度的变化,隧道段的最大有效应力变化不明显,这可以理解为部分延长或缩短隧道在一定程度上并不能影响抗反流效果。C型隧道类似于正常输尿管隧道形态,其模拟结果显示存在较小区域的高应力分布,但其缺乏Waldeyer鞘等重要结构的模拟,无法体现正常解剖下的应力分布。D型隧道位移分布云图提示其在排尿期可能存在抗反流作用,但在储尿期容易出现反流。
利益冲突 所有作者声明不存在利益冲突
作者贡献声明 万隆、吴文波负责文献检索;万隆、李满媛、吴文波负责论文设计,万隆、李满媛负责数据收集;万隆、吴文波负责论文撰写;吴文波负责知识性内容的审读与修正
| [1] |
Hutch JA, Ayres RD, Loquvam GS. The bladder musculature with special reference to the ureterovesical junc-tion[J]. Trans West Sect Am Urol Assoc, 1960, 27: 83-93. DOI:10.1016/S0022-5347(17)65374-6 |
| [2] |
Tullus K. Vesicoureteric reflux in children[J]. Lancet, 2015, 385(9965): 371-379. DOI:10.1016/S0140-6736(14)60383-4 |
| [3] |
中华医学会小儿外科学分会泌尿外科学组. 儿童原发性膀胱输尿管反流专家共识[J]. 临床小儿外科杂志, 2019, 18(10): 811-816. ediatric Urology Group, Branch of Pediatric Surgery, Chinese Medical Association. Expert consensus on management of primary vesicoureteral reflux in children[J]. J Clin Ped Sur, 2019, 18(10): 811-816. DOI:10.3969/j.issn.1671-6353.2019.10.002 |
| [4] |
Wein AJ, Kavoussi LR, Partin AW, 等. 坎贝尔-沃尔什泌尿外科学-第7卷-小儿泌尿外科学[M]. 夏术阶, 纪志刚, 杨屹, 等译. 第11版. 郑州: 河南科学技术出版社, 2020: 430-432. Wein AJ, Kavoussi LR, Partin AW, et al. Campbell-Walsh urology-volume 7-pediatric urology[M]. Xia SJ, Ji ZG, Yang Y, et al, translated. 11th ed. Zhengzhou: Henan Science and Technology Press, 2020: 430-432. |
| [5] |
王芳, 孔虎, 翟丽东, 等. 男性尿道括约肌失协同的有限元分析[J]. 医用生物力学, 2022, 37(1): 131-136. Wang F, Kong H, Zhai LD, et al. Finite element analysis of male urethral sphincter loss synergy[J]. J Med Bio-mech, 2022, 37(1): 131-136. DOI:10.16156/j.1004-7220.2022.01.020 |
| [6] |
Wyndaele JJ. Normality in urodynamics studied in healthy adults[J]. J Urol, 1999, 161(3): 899-902. |
| [7] |
Tekgül S, Riedmiller H, Hoebeke P, et al. EAU guidelines on vesicoureteral reflux in children[J]. Eur Urol, 2012, 62(3): 534-542. DOI:10.1016/j.eururo.2012.05.059 |
| [8] |
Stein R, Dogan HS, Hoebeke P, et al. Urinary tract infections in children: EAU/ESPU guidelines[J]. Eur Urol, 2015, 67(3): 546-558. DOI:10.1016/j.eururo.2014.11.007 |
| [9] |
Diamond DA, Mattoo TK. Endoscopic treatment of primary vesicoureteral reflux[J]. N Engl J Med, 2012, 366(13): 1218-1226. DOI:10.1056/NEJMct1108922 |
| [10] |
Chertin B, Puri P. Endoscopic management of vesicoureteral reflux: does it stand the test of time?[J]. Eur Urol, 2002, 42(6): 598-606. DOI:10.1016/s0302-2838(02)00447-5 |
| [11] |
Kim KW, Park SH, Im G, et al. CFD study on vesicoureteral reflux in the urinary tract with double J stent[J]. Comput Biol Med, 2022, 145: 105456. DOI:10.1016/j.compbiomed.2022.105456 |
| [12] |
Villanueva CA, Tong J, Nelson C, et al. Ureteral tunnel length ver-sus ureteral orifice configuration in the deter-mination of ureterovesical junction competence: a computer simulation model[J]. J Pediatr Urol, 2018, 14(3): 258.e1-258.e6. DOI:10.1016/j.jpurol.2018.01.009 |
| [13] |
Kalayeh K, Brian Fowlkes J, Schultz WW, et al. The 5:1 rule overestimates the needed tunnel length during ure-teral reimplantation[J]. Neurourol Urodyn, 2021, 40(1): 85-94. DOI:10.1002/nau.24526 |
 2024, Vol. 23
2024, Vol. 23


